일반물리학실험 | 파동의 중첩

 

 

 

TIP

 

 

파동의 중첩 원리와 리샤주 (Lissajous) 도형을 관찰하고, 이를 이해한다.

 

 

 

리사주도형(Lissajous’s figure)

1855년 프랑스 물리학자 J.A.리사주에 의하여 실험적으로 그 장치가 고안되었으며, 오늘날 레이저 쇼에서 사용되는 장치와 유사하다. x축 및 y축 방향에서의 단진동은 각각 x=Acosωt, y=Bcos(ω't＋δ)로 나타낼 수 있다. 진동수 ω 및 ω'의 비(比)나 위상차(δ)의 값에 따라 여러 가지 도형이 x-y 평면상에 그려진다. 평면 내에서 서로 수직인 2개의 단진동을 합성하여 얻어지는 2차원 운동의 자취를 나타내는 것이 리사주도형이다.

 

1. 주파수를 이미 알고 있는 신호를 Oscilloscope의 수평축에 입력한 후 측정하려 하는 신호를 수직 축에 접속, 생성된 패턴으로 두 주파수의 비를 알수 있다.

 

2. X-Y 모드에서 수평축과 수직 축에 다른 신호를 동시에 입력하면 리사주도형이 표시된다.

 

3. 두 신호의 주파수가 공약수를 가지고 있으면 파형이 안정되어 정지하며 주파수, 진폭, 위상을 비교 할 수 있다.

 

728x90

 

 

실험 방법

실험 1. 파동의 중첩

1) 함수 발생기 1과 2로부터 진동수가 각각 𝑓₁과 𝑓₂ 이고 진폭이 같은 두 사인파를 오실로스코프의 CH1과 CH2에 각각 넣는다. 이때 f₁ 과 f₂ 의 차이가 약 500Hz 이내가 되도록 한다.

 

2) ADD mode로 하면 두 파동이 합성된다.

 

3) TIME/DIV를 합성파가 잘 나타나도록 조절한다.

 

4) 화면에서 합성파의 진폭 주기의 반인 T₁/2 과 합성파의 주기 T₂를 측정하여 기록한다.

 

5) mode를 CH1만 놓고 오실로스코프에 나타난 파형으로 진동수 𝑓₁ 을 구하여 기록한다.

 

6) mode를 CH2만 놓고 오실로스코프에 나타난 파형으로 진동수 𝑓₂ 를 구하여 기록한다.

 

7) 맥놀이의 진동수 𝑓맥놀이 의 이론값과 실험값을 다음과 같이 계산한다.

 

𝑓(_이론) = ⟁⎥𝑓₁- 𝑓₂⎥

𝑓(_실험) = 2 /T₂

 

8) 𝑓맥놀이 의 상대 오차를 구한다.

 

9) 이번에는 합성파 진동수의 이론값과 실험값을 다음과 같이 계산한다.

 

𝑓(_이론) = (𝑓₁+𝑓₂ )/2

𝑓(_실험) = 1 /T₂

 

10) 𝑓합성의 상대 오차를 구한다.

 

11) 같은 방법으로 진동수를 두 번 더 달리하여 1) ～ 10)의 과정을 반복한다.

 

 

실험 2. 리사주(Lissajous) 도형

1) 진폭은 같고, 진동수는 다른 두 사인파를 CH1과 CH2에 입력시킨다.

 

2) 오실로스코프를 X-Y mode로 놓으면 리샤주(Lissajous)도형이 나타난다.

 

3) 우선 X,Y 축의 진동수를 각각 변화시키면서 여러 형태로 나타나는 리샤쥬 도형을 관찰하라.

 

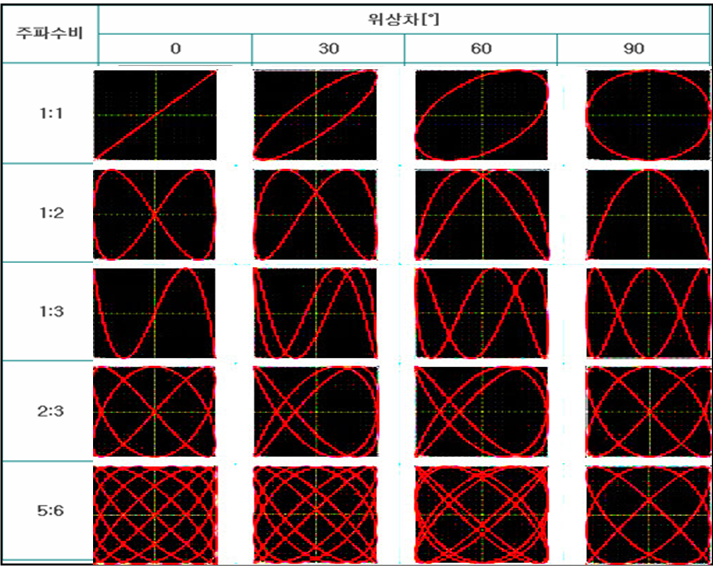
4) 함수 파형발생기 진동수의 비가 1:1, 1:2, 2:3의 경우, 위상 변화를 고려하면서 관찰한 리사쥬 도형을 그리고 각 축의 진동수를 각각 기록하라.

 

 

 

[일반물리학실험]파동의 중첩 레포트