전기물리학실험 | 커패시터 및 커패시터회로

 

 

 

TIP

 

 

1. RC의 회로에서의 실험적 시상수를 측정해 보자.
2. 저항과 축전기의 소자의 실제 값과 예측한 값의 시상수를 비교해 보자.

 

 

 

시상수

1차 지연 요소에서 입력 신호가 달라졌을 때 출력 신호가 정상 상태에 도달하기까지의 과도기간에서의 현상의 상태를 아는 가늠이 되는 상수. 예를 들면 전기 회로에서의 일례로서 R과 L의 직렬 회로에 대해서는 직류 전압 V를 가한 직후부터 시간 t의 경과에 의한 전류 i의 변화는

가 되어 그림과 같이 변화하는데, 이 때 전류가 정상값의 63.2%에 이르기까지의 시간 τ＝L/R[s]가 시상수이다. 일반적으로 시상수가 클수록 정상값에 이르기까지의 시간이 길어지고, 이 값은 제어계 또는 전기 회로의 조건에 따라서 결정된다.

728x90

 

 

실험 방법

1. 실험 절차

1) 회로를 <그림1>처럼 연결하고 10㎌ 축전기와 100㏀ 저항을 연결한다. 데이터 테이블에 저항값과 축전기의 값을 오차까지도 기록한다, 만약 버니어 회로판을 사용한다면 터미널 수가 아래 적혀 있으므로 회로를 구성하는데 도움이 될 것이다

 

2) 전압 센서를 랩프로 인터페이스의 1번 채널에 연결하고, 저항에 따라 연결되어 있는 축전기 쪽에 전압 센서의 적색 리드선(+)을 연결 한다. 흑색 리드선은 축전지의 다른쪽에 연결 한다.

 

3) Physics with Vernier 폴더에서 “24 Capacitors.cmbl” 파일을 연다.

 

4) 스위치를 <그림 1>처럼 연결하고 축전기를 30초 동안 5V 충전하여 전압 값을 얻는다. 전압이 계속 증가하는 것을 볼 수 있다. 전압이 상수가 될 때까지 기다린다.

 

5) 수집 버튼을 눌러 자료 수집을 시작한다. 그래프가 시작되자마자, 축전기를 방전하기 위해 스위치를 다른 위치로 바꾼다. 데이터는 상수 값을 초반에 보일 테지만, 감소하는 함수가 될 것이다.

 

그림 1 실제 회로 구성도

 

6) 모델과 데이터를 비교하기 위해, 그래프에서 전위가 감소하기 시작하는 부분을 드래그하여 선택하고 상수 부분을 뺀다. 곡선 추세선 버튼을 눌러 함수 박스에서 자연 지수 함수를 선택한다(A*exp(-Ct)+B). 맞춤 테스트 버튼을 눌러 확인해본다. 확인 버튼을 눌러 메인 그래프 창으로 돌아간다.

 

7) 데이터 테이블에 고정시킨 변수 값을 기록한다. 곡선 추세선에 쓰는 C는 일상적으로 쓰는 축전기가 나타내는 C가 아니다. 앞에서 설명한 식에서 축전기의 방전에 관한 수학적 모델과 맞춤 방정식을 비교하여 보자.

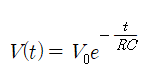
회로의 시상수와 상수 C는 어떤 관계에 있는지 알아보고 어느 쪽이 소개에서 정리를 내릴 수 있는가?

 

 

8) 전압-시간 그래프를 인쇄하거나 스케치하고 마지막으로 실행한 값을 저장한다. 이것은 나중에 분석을 위해 필요하다.

 

9) 축전기는 이제 방전되었다. 충전 과정의 모니터를 위해 수집 버튼을 누른다. 자료 수집이 시작되자마자 스위치의 방향을 바꾼다. 데이터 수집이 완료된다.

 

10) 축전기의 충전과정에 대한 수학적 모델과 데이터를 비교해 보자.

 

11) 데이터 테이블에 고정 매개 변수들을 기록한다. 충전된 축전기에 대한 수학적 모델과 방정식을 비교하여 보자.

 

12) 데이터 메뉴에서 데이터 세트 숨기기를 선택하여 첫 번째 실행을 숨긴다. 왼쪽 코너 위에 있는 대화 박스를 클릭하여 남아 있는 정보를 지운다.

 

13) 낮은 저항을 사용하여 반복실험을 해보자. 이 변화는 축전기 방전 방법에 어떠한 영향을 미치는지 알아보자. 47㏀의 저항을 사용하여 회로를 다시 구성하고, 실험 단계 4~11을 반복해 보자.

 

 

 

[전기물리학실험]커패시터 및 커패시터회로 레포트