일반물리학실험 | 에어트랙(Air Track)

 

 

 

TIP

 

 

마찰이 없는 수평 미끄럼판에서 운동하는 물체의 여러 가지 역학적 현상을 관찰한다.

 

 

 

에어트랙(air track)은 압축 공기를 수많은 작은 구멍을 통하여 분출시켜 활차(glider)를 뜨게 함으로써 활차가 마찰이 없이 움직이게 만들어 주는 장치이다. 따라서 마찰이 없는 이상적인 조건하에서 물체의 병진운동, 진동, 충돌 등을 관찰할 수 있으며, 이와 관련된 여러가지 역학법칙 및 보존법칙 등을 확인할 수 있다.

728x90

 

 

실험 방법

1. Newton의 제 2법칙

1) 아래 그림과 같이 에어트랙의 수평을 잘 맞추어 설치하고 양쪽 끝 가까운 위치 x₁과 x₂에 포토게이트 계시기와 부속 포토게이트를 놓는다.

 

2) 활차의 질량 m과 추걸이의 질량을 각각 확인하여 기록하고, 활차와 추걸이를 실로 연결한다.

 

 

3) 추걸이에 10g 짜리 추 2개, 1g 짜리 추 2개 (또는 5g 짜리 추 2개, 2g 짜리 추 2개)를 올려 놓는다. 추걸이의 질량과 얹어놓은 추의 질량을 합하여 얻어지는 총 질량 M을 기록한다.

 

4) 포토게이트 계시기를 PULSE MODE에 놓는다.

 

5) 포토게이트 계시기가 있는 위치 x₁을 활차의 시발점으로 정하여 활차를 올려놓고 (주의: 활차 위의 끝이 포토게이트의 레이저 구멍에 최대한 근접하게 위치시킨다. 이때 포토게이트의 계시기가 작동하지 않도록 주의한다.) 활차가 추의 힘으로 미끄러지지 않게 잡고 있는다.

 

6) 포토게이트 계시기의 RESET 버튼을 누른 다음, 잡고 있던 활차를 살며시 놓아준다.

 

7) 활차가 첫번째 포토게이트를 통과하면 계시기의 시간이 기록되기 시작하여 두번째 포토게이트를 통과하면 시간이 멈춘다. 이때 걸린 시간 △t를 계시기에서 읽어서 기록한다.

 

8) 다시 x₁의 위치에 활차를 놓고 위의 과정을 5회 반복하여 △t의 평균값을 구한다.

 

9) 양쪽 포토게이트의 위치 x₁과 x₂를 읽어서 기록하고, △t와 D=|x₂-x₁|로부터 식 (3)을 이용하여 가속도를 구한다.

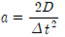
10) 추(추걸이를 포함한)의 질량 M, 활차의 질량 m, 중력가속도 g로부터 계산되는 식 (2)의 가속도 a=Mg(m+M)과 위에서 구한 가속도를 비교하고 어느 값이 더 정확한 값일까를 생각해 보라.

11) 위의 전체 과정을 추의 질량과 활차의 질량 및 포토게이트의 위치를 적당히 바꾸어 가면서 반복해 보라.

 

2. 완전 비탄성 충돌에서의 운동량 보존 법칙

1) 에어트랙을 그림과 같이 수평으로 설치한다.

 

2) 트랙의 한쪽 끝에 질량 m₁의 활차의 출발점 x₀을 설정한다.

 

 

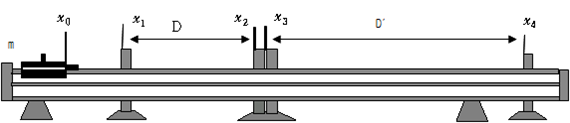
3) x₁과 x₂, 그리고 x₃과 x₄를 그림과 같이 적당한 간격으로 설정하고 x₁과 x₂에 한 쌍의 포토게이트 계시기와 부속 포토게이트를, 그리고 x₃과 x₄에 또 한 쌍의 포토게이트 계시기와 부속 포토게이트를 놓는다. 이때 x₂와 x₃의 위치를 최대한으로 밀착시켜 본 실험에서 생길 수 있는 불필요한 간격으로 인한 오차의 소지를 최소화하도록 한다. 각 포토게이트의 위치 x₁과 x₂, 그리고 x₃과 x₄를 읽어서 기록해 둔다. D=|x₂-x₁|과 D’=|x₄-x₃|이 나중에 각각 충돌 전과 후의 활차의 속도 계산에서 그 이동거리로 처리된다.

 

4) 두 활차의 질량 m₁과 m₂를 각각 확인하여 기록한 다음, 질량 m₁인 활차를 앞에서 정한 출발 위치x0에 올려놓고, 이 질량 m1인 활차의 끝이 x₂를 통과할 때 질량 m₂인 활차와 충돌할 수 있도록 질량 m₂인 활차를 위치 x₃에 올려 놓는다. 질량 m₁인 활차에는 뾰족한 침이 있고 질량 m₂인 활차에는 고무가 있는 액세서리가 부착돼 있어서 충돌 후 두 활차가 붙어서 함께 운동하게 되어있다.

 

5) 양쪽 포토게이트 계시기의 스위치를 PULSE MODE에 놓는다. 충돌 전의 운동 시간은 x₁의 포토계시기가, 충돌 후의 운동 시간은 x₃의 포토계시기가 측정하게 된다.

 

6) 양쪽 포토게이트 계시기의 RESET 버튼을 누른다.

 

7) x₀의 위치에서 질량 m1인 활차를 잡고 있다가 살며시 밀어서 출발시킨다.

 

8) 질량 m₁인 활차가 앞에 있는 한 쌍의 포토게이트를 지나가는데 걸리는 시간 △t와 충돌 후에 붙어서 움직이는 두 활차가 뒤에 있는 한 쌍의 포토게이트를 지나가는데 걸리는 시간 △t′을 각각의 계시기에서 읽어서 기록한다.

 

9) 위의 과정 4) ― 8)을 5회 반복하여, △t의 평균값과 △t′의 평균값을 구한다.

 

10) 위의 △t와 △t′및 이에 대응하는 이동거리 D=|x₂-x₁|과 D’=|x₄-x₃| 을 이용하여 충돌 전의 질량 m₁인 활차의 속도 v=D/△t와 충돌 후에 붙어서 움직이는 두 활차의 속도 v′=D′/△t′을 구하고, 운동량 보존 법칙의 관계식 (6)이 지켜지는지를 확인한다.

 

11) 거리 D와 D′을 각각 10㎝ 정도씩 줄이면서 과정 3) ― 10)을 반복하고, 역시 운동량 보존 법칙이 만족되는가를 확인한다.

 

 

 

[일반물리학실험]에어트랙(Air Track) 레포트