
픽의 확산법칙은 열역학에서 확산을 물리적으로 분석하기 위해 19세기 독일의 생리학자 아돌프 오이겐 픽이 1855년에 밝혀낸 법칙이다. 픽의 제1법칙의 도식화 픽의 제1법칙은 입자의 확산유량과 입자의 농도의 변화량과의 관계를 기술한 법칙이다. 계의 부피가 일정하다는 조건 하에서 직교좌표계에서 x축으로 입자가 확산될 때, 두 물리량의 관계는 다음과 같다
Fick 의 제 1법칙(Fick`s first law)
확산의 양은 거리에 따른 농도차(농도기울기)에 좌우된다. 즉, 농도차가 클수록, 거리가 가까울수록 확산의 양은 증가한다.
x 지점에서의 확산의 양은,
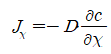
Jx : 확산의 순운동(net flux), D : 확산상수(diffusion coefficient)
확산율(diffusivity), c : 농도차, x : 거리차
Fick의 제 2법칙(Fick`s second law)
Fick의 제 1법칙에 시간의 개념을 추가한 방정식이다. 즉, 어떤 특정한 점의 농도기울기는 시간에 지남에 따라 제 1법칙에 따라 농도가 변하므로 그 일시적인 농도기울기의 시간에 대한 변화율을 반영한 식으로 거리에 대한 2차 미분방정식이 된다.
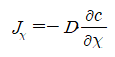
다음 평면을 지나는 확산의 유량은
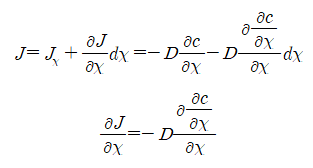
거리에 대한 유량의 변화는 시간에 대한 농도의 변화 즉, -c/t이다.
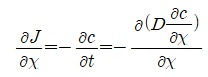
확산상수 D가 농도에 의존하지 않는 독립적인 일정한 값일 경우에는
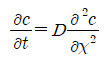
式이 성립한다.
미분 방정식의 해는
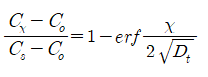
erf : Gaussian error function, c0 : 초기체적농도, cs : 표면농도
따라서 이를 이용하면 포화되는데 필요한 시간도 도출해낼 수 있다. 또한 같은 확산상수를 갖더라도 기하학적인 형상에 따라 확산속도 및 포화에 필요한 시간이 다르게 나타난다
간략히 설명하면, 확산이란 기체분자나 원자, 고체/액체 상태를 구성하는 원자가 화학포텐셜(chemical potential)차이에 의해 화학포텐셜이 높은 곳에서 낮은 곳으로 구성입자가 이동하는 현상을 말합니다. 그런데 대부분의 경우, 화학포텐셜은 농도에 비례합니다. 즉, 대부분의 경우에는 농도가 높은 곳에서 낮은 곳으로 확산을 하게 된다는 것입니다. 이러한 경우에, 농도구배(단위길이당 농도의 변화)에 따른 확산 flux를 예상하는 법칙이 Fick의 법칙입니다.
1차원인 경우, 제 1법칙은 다음과 같이 나타낼 수 있습니다.
Fick의 제 1법칙 :
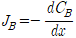
J는 단위시간당 단위 면적을 지나는 원자의 수를 나타내는 Flux이고, DB는 B 원자의 확산계수, C는 농도 x는 방향, dCB/dx는 x방향으로의 농도 변화율을 나타냅니다.
정상상태의 경우에만 적용할 수 있습니다. (정상상태란 시간에 따른 농도의 변화율 dC/dt=0인 상태를 말합니다). 정상상태에서 flux는 일정하게 유지되고, 이 때 확산은 농도구배(농도차)가 클수록 잘 일어나며 농도가 높은 곳에서 낮은 곳으로 확산이 일어난다는 것을 알 수 있습니다.
제 2법칙은 비정상상태(시간에 따라 농도가 변화하는 경우 dC/dt값이 0이 아닌경우)의 경우에 시간에 따른 농도 변화를 예측하는 법칙입니다.
Fick의 제 2법칙 :
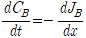
JB값은 Fick의 제1법칙과 같이 표현되는데, 확산계수 D가 농도에 상관없이 일정한 경우 위식은 다음과 같이 표현할 수 있습니다.

이 식의 의미는, 농도의 2차 미분항이 양의 값을 가지는 경우에 그 위치에서는 시간에 따라 B원자의 농도가 높아짐을 의미합니다. (반대로 음의 값을 가지는 경우에는 시간에 따라 감소). 즉, 위치에 따른 농도를 그래프로 나타내었을 때, 위로 볼록한 부분(2차 미분값이 0보다 작다)은 시간이 지남에 따라 농도가 감소하고, 아래로 볼록한 부분(2차 미분값이 0보다 크다)은 시간이 지남에 따라 농도가 증가하여 전체적으로 농도가 일정하게 됨을 알 수 있습니다.
확산 (Diffusion)
확산과정은 Fick법칙을 따른다.
1차원(즉 x방향)에서 Fick's 1'st law는 다음과 같다.

여기서 J는 확산종의 flux로서, 보편적 단위는 단위시간, 단위면적 당의 확산종의 수, 몰, 또는 질량, 즉 #/㎠sec, g/㎠sec, mole/㎠sec이다. C는 농도로서 단위부피 당의 수, 몰, 또는 질량, 즉 #/㎤의 단위를 갖는다.
일반적으로 확산계수는 재료에서 방향의 함수이다. 그러나 유리는 등방성이므로, 이것은 문제가 되지 않는다. Fick의 1법칙은 J와 ∂C/∂x가 일정한 정상상태에서 사용된다.
비정상상태에서는 Fick's 2'nd law가 사용된다.
1차원 경우에
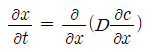
이는 다음과 같이 유도할 수 있다. 다음 그림에서 보이듯 농도변동이 존재하는 단위 단면적의 막대를 다루자.
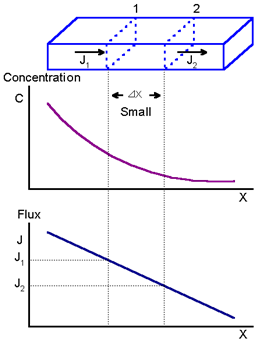
두 평면 1과 2가 작은 거리 x 떨어져 있을 때,
이들 평면에서의 flux J1과 J2 는 다음과 같이 관련된다.
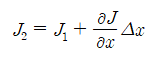
평면 1과 2사이 작은 부피요소(volume element) 경우에 J1은 부피요소로 들어가는 flux이고 J2는 이 부피요소에서 나가는 flux이다. 따라서 단위시간에 부피요소에 확산하는 종의 net increase는

이는 시간에 따른 부피요소 내에서의 확산하는 종의 양의 변화와 같다. 즉
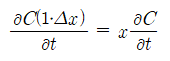
여기서 1·Δx는 고찰하의 부피요소이다. 위 식으로 부터

식에 Fick's 1'st law를 대입하면, Fick's 2'nd law가 얻어진다. 만약 확산계수 D가 농도에 무관하다면(이는 C가 x의 함수이므로 D 또한 x에 무관하다는 것을 의미한다) 위식은 다음과 같이 된다.
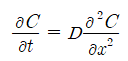
Fick's 2'nd law의 해는 경계조건아래 풀어야 한다. 여기서는 두가지 경우의 해를 논의한다.
1. Thin film on a semi-infinite bar
작은 양의 확산종이 긴 막대의 표면상에 있을 때, 확산종의 농도는 시간 t와 깊이 x의 함수로 다음과 같이 주어진다.
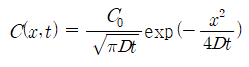
여기서 C0는 초기의 표면농도이다. 확산종이 두 개의 긴 막대사이에 sandwich 되어있고 두 방향으로 확산할 수 있다면, 위식의 오른쪽 항은 2로 나누어야 한다.
2. Constant surface concentration
재료의 표면에 확산종의 무한 source가 있을 때, 재료의 농도는 다음과 같이 주어진다.
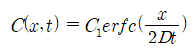
여기서 C1은 constant concentration이고
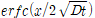
는 다음과 같이 정의되는 conjugate error function이다.
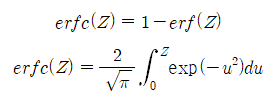
이들 식에서 Z는 변수, u는 적분변수이고 erf(Z)는 error function이라고 부른다. erf(Z)는 다음의 성질을 갖는다.
erf(∞) = 1 erf(0) = 0 erf(-Z) = - erf(Z)
위 식의 양 해에서 확산계수 D는 항시 Dt로서 t와 함께 나타난다. 양 Dt는 확산거리(diffusion distance)라고 불리우며, 확산의 평균깊이(average depth)의 근사적 척도를 나타낸다.


댓글