생체역학실험 | 모멘트 법칙

힘의 평형을 이루고 있는 물체(빔) 에 여러 힘을 가하여 힘의 평형을 이루게 한 후 모멘트의 법칙으로 이를 검증하는 실험이었다. 어떤 힘이 가해져 회전 운동이 발생했을 경우, 이 회전 운동 값은 힘 F, 축과 힘의 작용선 r의 곱으로 나타낼 수 있는데 이를 힘의 회전모멘트라고 하며, 서로 반대 방향으로 여러 힘이 작용하여 힘의 회전모멘트의 합이 같을 경우 물체는 정지하게 되는데 이를 모멘트 법칙이라 한다.

 

∑M(cw) = ∑M(ccw)

 

힘이 가해져 회전 운동이 발생할 경우, 이 회전 운동 값은 W와 A의 곱인 (W x A)로 나타낼 수 있다. 여기서 W는 힘을 나타내며, A는 축과 힘의 작용선까지의 수직 거리를 나타낸다. (그림 1 참고) (W x A)를 힘의 회전모멘트(회전모멘트)라고 한다.

 

 

물체에 여러 힘이 서로 반대 방향으로 가해질 경우, 각 방향의 회전모멘트의 총 합이 같을 경우 이 물체는 회전하지 않는다. 이를 모멘트 법칙(principle of moments)이라고 한다.

 

모멘트 법칙은 회전 운동을 방지하기 위해 힘이 서로 균형을 이루어야 하는 공학 및 건설 관련 문제에서 자주 사용된다. 모멘트 법칙은 평행한 힘 및 경사 방향의 힘 모두 적용되며, 회전모멘트를 계산할 경우 길이 A는 힘 W의 작용선으로부터 축까지의 수직 거리를 나타낸다. 회전력이 서로 평형을 이루는 공식은 아래와 같다.

 

시계 방향의 모멘트 총 합 = 반시계 방향의 모멘트 총 합

 

 

실험 방법

실험 1

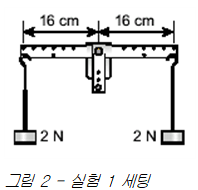
웨이트 훅(P10)을 바의 양단 구멍에 그림 2와 같이 매단다. 이때 훅이 바의 뒤에서 앞쪽으로 걸리게 한다. 웨이트 훅의 무게는 각각 0.1N이며, 1.9N의 하중을 추가해 총 하중이 각각 2N이 되도록 한다. 바가 스톱 사이를 움직이는 센터 암에 대해 계속 수평을 유지하고 있는지 확인한다. 바의 축에서부터 웨이트 훅까지의 거리를 측정한다. 이 거리는 160㎜이어야 한다.

 

 

우측의 웨이트 훅을 축 방향의 구멍 쪽으로 이동하고 적절한 무게를 추가해 바가 수평이 되도록 한다. (그림 3 참고) 이동한 웨이트 훅의 총 무게(W)를 기록하고 축에서 구멍까지의 거리(A)를 기록한다.

 

 

실험 2

줄의 길이가 대략 40㎝가 되도록 한다. 우측 웨이트 훅을 바에서 제거한다. 이 줄을 중심부의 풀리(P12)에 걸치고 바의 우측 암의 끝 단 구멍에 줄을 매단다. (그림 4) 이때 경량 훅(P11)을 이용한다. 웨이트 훅 및 하중을 가하고, 바가 수평이 되었을 때, 축에서부터 줄까지의 수직 거리를 측정한다.

 

 

좌측 풀리에 줄을 걸치고 바의 센터 암의 가장 아래쪽 구멍에 연결해서 실험을 반복한다. (그림 5 참고)

 

 

 

 

[생체역학실험]모멘트 법칙 레포트